An important part of performing the asset value calculation is accounting for asset treatments and their effects. Treatments are important in two basic ways:
- It is important to consider what treatments are typically performed on an asset to determine an asset’s useful life and “residual value,” or value when an asset reaches the end of its useful life.
- In some cases, one may wish to specifically include additional treatments in the asset value calculation besides asset acquisition/construction and reconstruction. This is particularly important if one is predicting future asset value.
To calculate asset value, one should establish what treatments are performed on an asset. An asset lifecycle strategy describes the different treatments that are typically performed on an asset following its initial construction or acquisition. Defining a lifecycle strategy is consistent with best practice in TAM. Also, State DOTs are required to define lifecycle strategies for pavements and bridges in their NHS TAMP.
At a minimum, basic information on what asset treatments are typically performed on an asset is useful in establishing asset life and residual value as described further in subsequent subsections of this chapter. For instance, for the purpose of valuing service vehicles, one would set the life of the asset assuming that various treatments are conducted based on the asset’s lifecycle strategy, such as routine maintenance and replacement of brakes, tires and other vehicle components.
For certain applications it may be necessary to go a step further, and include the costs and effects of various asset treatments explicitly in the asset value calculation. This is particularly important if the intended application of the asset value calculation is to predict future asset value. In this case one may wish to account for what treatments are expected to be performed, and may wish to compare treatment strategies. In this case there are two reasons may wish to include a given treatment in the calculations:
- Specifying the Impact of Treatments on Remaining Asset Life. For some complex assets, such as pavement and bridges, treatments may be performed – short of outright replacement of the asset – that have a significant impact on the remaining asset life. For instance, if a pavement is overlayed or a bridge is rehabilitated, its useful life is expected to be much longer than if these treatments are not performed. In these cases, incorporating past treatments may yield a more accurate calculation of current asset value – if sufficient data are available to support the calculation.
- Demonstrating Effects of Treatments on Future Value. If the asset value calculation is being performed to demonstrate the effects of a given treatment, then the treatment needs to be accounted for in some manner to show how the value changes if the treatment is performed. For instance, one might calculate future asset value with and without performing the treatment.
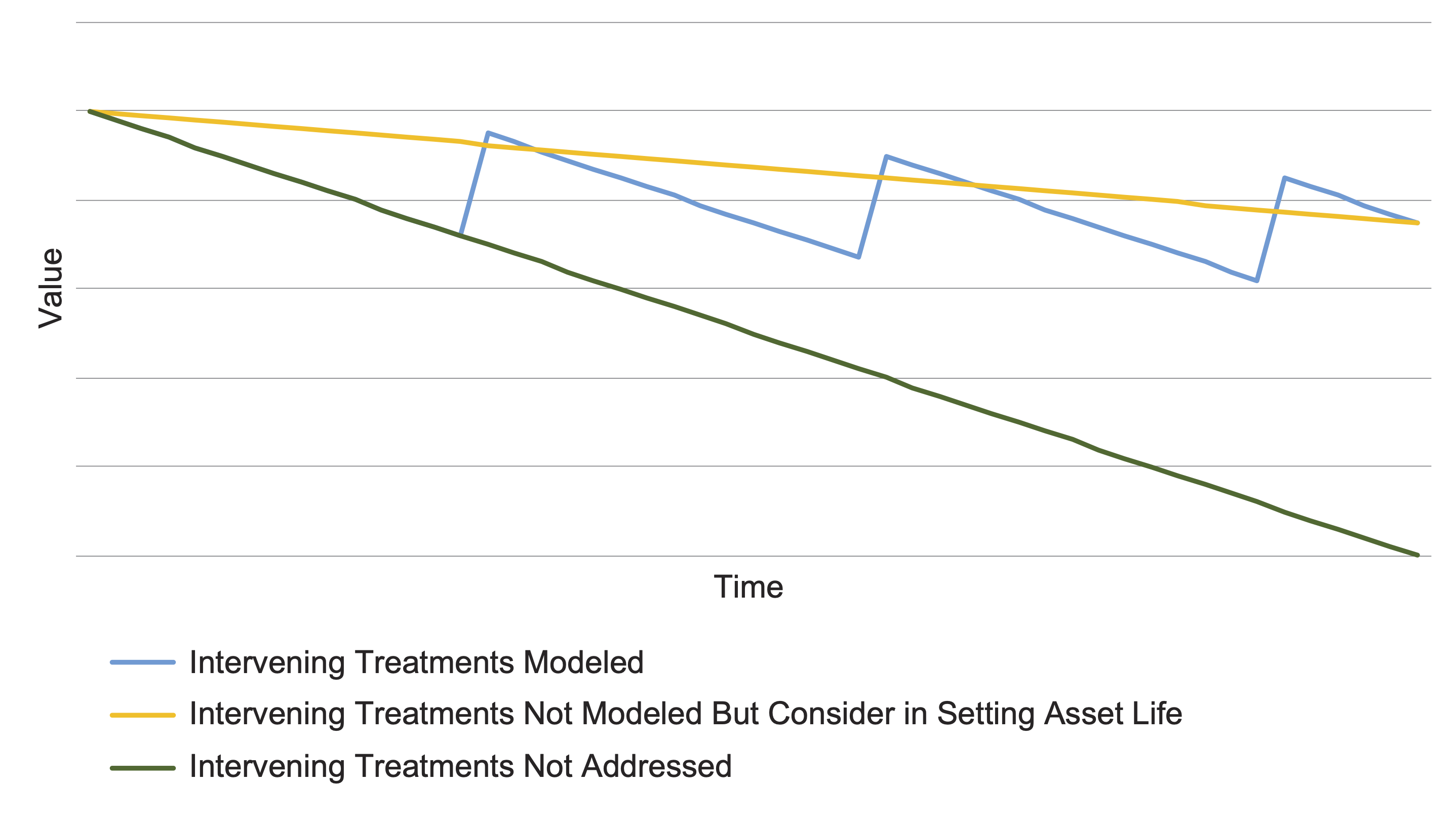
Figure 5-1, adapted from the Edgerton’s discussion of this topic (12), illustrates the importance of considering renewal treatments for certain assets, referred to by Edgerton as “cyclical maintenance assets.” This figure shows three lines illustrating the value of an asset over time. The jagged line in the figure below shows asset value if renewal treatments are explicitly modeled: these add value and add life to the asset. The straight upper line shows how asset value is calculated if the effect of renewal treatments is approximated through a revised estimate of asset life. In this case, asset treatments are not explicitly modeled. The lower line is demonstrably incorrect. In this case, renewal treatments are not modeled, but the asset life has not been modified to account for these treatments. This results in systematic understatement of asset value.
To determine what treatments to model it can be helpful to review multiple sources, such as guidance on what treatments are recommended for an asset, models in an agency’s management systems, and the data an agency actually tracks on its treatments. This is complicated since the same treatment may be represented in different ways between different organizations and/or systems.
For other applications where the goal is to calculate current asset value, it is generally not necessary to explicitly account for all of the different treatments that have been performed on an asset in the past. It is recommended that defining additional treatments be avoided in this case if possible. However, one may wish to consider additional treatments if value is based on historic costs, or if the depreciation approach is based on the actual time since the last treatment. Depreciation is discussed further in Chapter 6.
For each treatment that is modeled one must establish how much the treatment costs and what effect the treatment has on an asset. The approaches described in Chapter 4 for calculating replacement costs are equally applicable to calculating the cost of other treatments. Generally speaking, the calculation of treatment costs should be made in today’s dollars (constant dollars), removing the effects of inflation from the analysis. This approach allows for directly comparing costs incurred at different times. If calculations are made in current rather than constant dollars, one must be careful to state the year of the expenditure and avoid comparing costs in different years without inflation adjustments. However, in the case that one is basing asset value on historic costs all costs should be expressed in year of expenditure dollars.
Concerning treatment effects, the most straightforward case to consider is that the treatment has the effect of restoring the asset to “like new” condition, resetting its age to 0. Alternatively, a treatment might extend the life of the asset and/or improve its conditions. Both of these effects can be translated into a change in the effective age of the asset. If the impact of the treatment cannot be translated into a change in condition or effective age then it should not be explicitly considered.
When considering treatments and their effects, a key issue is how assets have been componentized. If a complex asset is represented using components, then this may simplify the specification of treatment effects, and allow for the consideration of additional treatments. For example, a common treatment for a bridge is to rehabilitate or replace the bridge deck, which resets the age of the bridge deck but may not impact the age of the bridge superstructure or substructure. If a bridge is represented in components consisting of a deck, superstructure and substructure, then the effect of a deck replacement can be easily modeled: it resets the age of the deck to 0 and improves its condition to a “like new” condition. If one is modeling the overall bridge, then the effect of a deck replacement is more difficult to ascertain. One can approximate the effect in this case, or simply assume that deck replacement occurs on a regular cycle and not attempt to model this treatment.
Once the analyst makes a decision about what treatments to explicitly model and what treatments are assumed to occur over the life of an asset, they can then establish the asset’s expected useful life. Asset life is an important parameter for the depreciation calculation described in Chapter 6.
The goal here is to determine how long the asset would be expected to remain in service provided:
- An asset is removed from service either when it is more cost effective to replace the asset or when it is obsolete;
- The treatments that are assumed to occur in the analysis actually do occur, including planned maintenance, cyclical treatments that are needed to achieve the asset’s useful life, and any other treatments that may impact the life of the assets if they are omitted; and
- The life-restoring treatments distinguished from general maintenance are not assumed to occur, as their contributions to asset value and life will be accounted for separately.
The above criteria have some important implications. One is that we are not concerned with how long an asset would remain in service in the abstract case that no treatments are ever performed on an asset. Instead, we would like to know what the useful life is given treatments such as routine maintenance are performed. But this means that estimates of useful life are contingent on the assumed set of treatments performed on an asset, also called the agency’s lifecycle strategy for the asset.
Another implication of the above criteria is that it is completely feasible for an asset to remain in service past its useful life. This may occur because it is still cost effective to maintain a specific asset, or because it has simply not been feasible to replace the asset and it continues to be maintained despite the fact that a replacement may be more cost effective.
Assets of historical significance are unique in this manner, for they are maintained beyond the useful life that would otherwise be defined for them. These assets require special treatment. Specific estimates may be required of the time until major rehabilitation action is required to retain such assets in service – or such assets can be componentized.
Various references are available which summarize typical useful lives of transportation assets and provide techniques for calculating agency-specific values. Two references are of particular note. Volume 1 of NCHRP Report 713 (18) is a guidebook for measuring the life expectancy of transportation assets. This report details how to define asset end-of-life, describes quantitative approaches for establishing asset life, and presents typical values for selected asset classes.
The OECD manual Measuring Capital (11) summarizes approaches for estimating useful lives for the purpose of calculating asset value, including techniques, such as development of Winfrey Mortality Functions and Weibull distributions. It also presents typical values for different asset classes based on a review of the literature. One application described in this manual uses an assumed distribution to approximate the age distribution of an asset inventory where detailed data are unavailable. For TAM applications it is assumed that sufficient data are available to determine the age distribution of an asset inventory, but the reader should consult the discussion in Chapter 12 of Measuring Capital where this is not the case.
Table 5-1 below summarizes typical useful lives for transportation assets based on NCHRP Report 713, Measuring Capital, NCHRP Synthesis 371 (19), and FTA guidance for vehicles (33). As noted above, all of the assumptions regarding asset life are assumed to incorporate a given treatment strategy. One should review the assumptions and their own data carefully when performing an analysis.
Table 5-1. Typical Useful Life Values for Transportation Assets
| Asset Class | Component | Typical Useful Life (years) | Notes |
|---|---|---|---|
| Pavement | Overlay - Asphalt | 11-20 | NCHRP Report 713 Vol. 1 (summary of the literature) |
| Overlay - Concrete | 20-34 | ||
| Full Depth - Asphalt or Concrete | 50 | ||
| Bridges | Deck | 58-79 | NCHRP Report 713 Vol. 2 (time to reach a rating of 3 or 4 based on model fit to NBI data) |
| Superstructure | 64-83 | ||
| Substructure | 59-78 | ||
| Culverts | Pipes | 50 | NCHRP Synthesis 371 (mode of survey results) |
| Box Culverts | 55-85 | ||
| Traffic Signals | Signal Head | 15 | NCHRP Report 713 Vol. 2 (time to reach a rating of 3 or 4 based on model fit to NBI data) |
| Structural Components (stell or aluminium) | 25-30 | ||
| Traffic Detector | 10 | ||
| Traffic Controller | 15 | ||
| Traffic Controller Cabinet | 20 | ||
| Lighting | Structural Components (steel or aluminium) | 25-30 | NCHRP Synthesis 371 (mode of survey results) |
| Ballast | 10 | ||
| Control Panels | 20 | ||
| Signs | Sheeting | 15 | NCHRP Synthesis 371 (mode of survey results) |
| Sign Posts (steel or wood) | 10-15 | ||
| Overhead Sign Structure | 30 | ||
| Sidewalks and Curbs | Asphalt | 10 | NCHRP Synthesis 371 (mode of survey results) |
| Concrete, Block or Brick | 20 | ||
| Vehicles | Automobile | 8 | FTA Useful Life Benchmark (ULB) Defaults |
| Cutaway Bus | 10 | ||
| Bus | 14 | ||
| Light or Heavy Rail Vehicle | 31 | ||
| Commuter Rail Coach or Locomotive | 39 | ||
| Ferryboat | 42 |
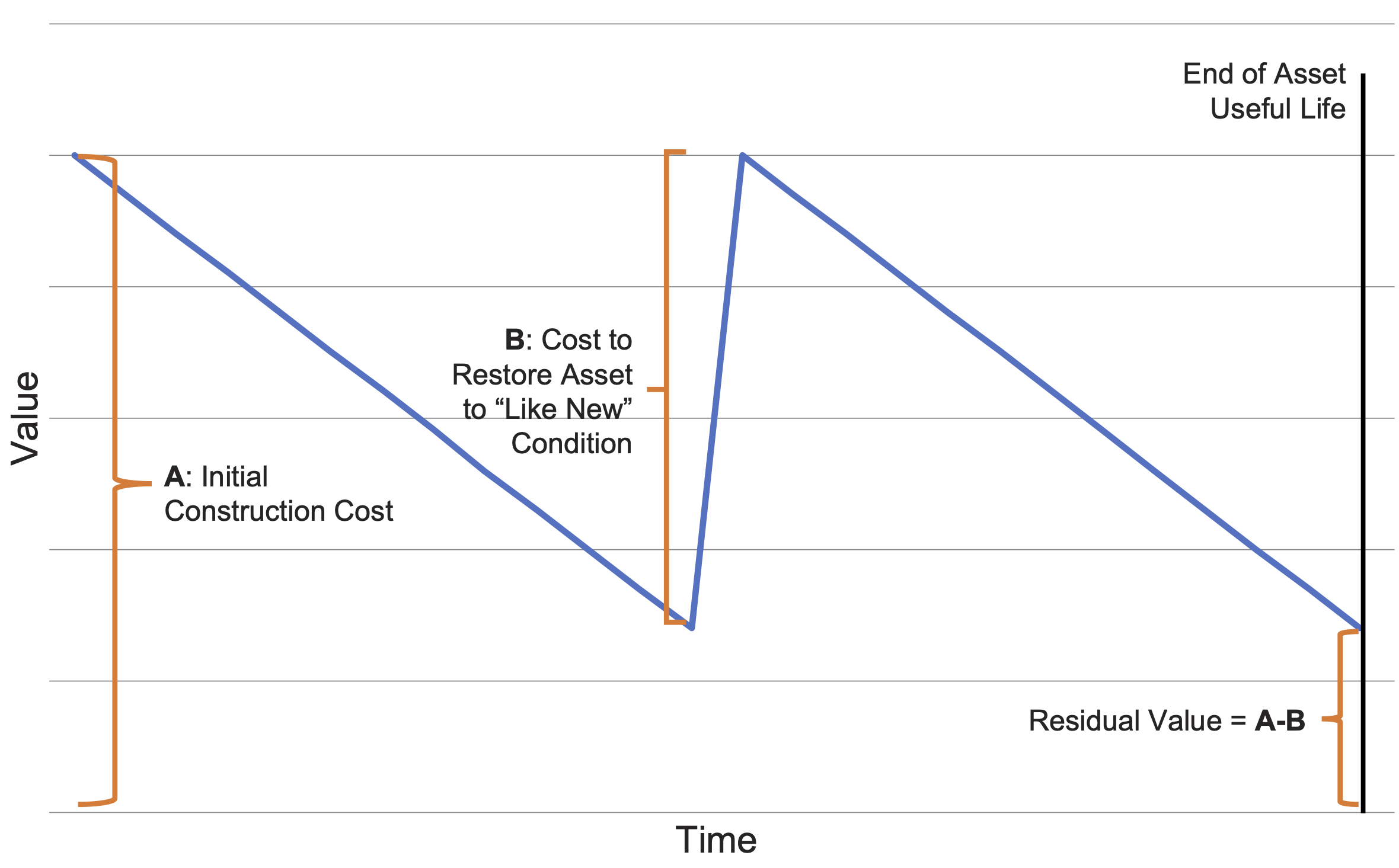
The final topic addressed in this portion of the asset value calculation is the determination of the residual value of the asset, or the value of the asset once it has reached the end of its useful life. Note this topic is addressed separately for the case where one calculates economic value, as discussed in Chapter 4. When one calculates value using a cost or market perspective, two basic approaches may be considered for determining this parameter: calculating the salvage value of the asset or calculating the cost to restore the asset to “like new condition.”
For assets that are completely replaced at the end of their useful life, the residual value should be based on the salvage value of the asset and may be 0. For instance, the salvage value for a vehicle might be set based on the price expected at auction. Assets that are discarded at the end of their life and not repurposed in some way have a salvage value of 0.
A different approach is recommended in cases where an asset is periodically rehabilitated and restored to a “like new” condition at a cost less than the initial construction or acquisition cost. In these cases, it is recommended that the residual value is equal to the difference between the cost of replacing the asset and the cost to restore the asset to “like new” condition at the end of its useful life. This approach is illustrated below in Figure 5-2. As demonstrated in the figure, this approach has the effect of restoring the value of the asset to that of a new asset when a complete rehabilitation treatment is applied. This method includes the aspects of an asset that do not depreciate or which depreciate very slowly in the residual value, such as foundations and earthworks, design, and land. Note that in this example it is assumed that the asset is restored to “Like New” condition. However, depending on the asset and treatment it may or may not be feasible to restore the asset to this condition.