The following are hypothetical examples illustrating application of the steps described in Section 4.2.
For pavement an agency decides to base its calculation of initial asset value on reconstruction cost using pavement lane miles as the unit of measure. Table 4-2 shows the data obtained to compute a unit cost for pavement in millions of dollars per lane mile for a given subtype and network. The table lists data for a set of pavement reconstruction projects. For each it shows the project year, quantity of pavement reconstructed in lane miles, project cost in year of expenditure dollars, and project cost in 2020 dollars. Project costs were inflated to 2020 costs using the Engineering News Record (ENR) Construction Cost Index.
Table 4-2. Example Data for Past Pavement Reconstruction Projects
| Project | Year | Description | Cost - Year of Expenditure ($M) | Cost - 2020 ($M) | Lane Miles (LM) | Unit Cost (2020 $M/LM) |
|---|---|---|---|---|---|---|
| 1 | 2010 | Route 80 MP 1.9 | 52.6 | 68.5 | 24.0 | 2.9 |
| 2 | 2016 | Route 84 MP 0.6 | 13.5 | 15.0 | 3.6 | 4.2 |
| 3 | 2007 | Route 92 MP 2.6 | 27.0 | 38.9 | 10.2 | 3.8 |
| 4 | 2011 | Route 101 MP 4.7 | 35.6 | 45.0 | 6.3 | 7.1 |
| 5 | 2005 | Route 101 MP 7.1 | 180.0 | 277.2 | 32.0 | 8.7 |
| 6 | 2014 | Route 104 MP 18.6 | 25.7 | 30.1 | 4.2 | 7.2 |
| 7 | 2009 | Route 104 MP 19.9 | 12.0 | 16.1 | 1.8 | 8.9 |
| 8 | 2017 | Route 680 MP 5 | 42.1 | 45.0 | 19.6 | 2.3 |
| 9 | 2013 | Route 680 MP 12 | 28.3 | 34.0 | 8.0 | 4.3 |
| 10 | 2018 | Route 780 MP 15.5 | 28.0 | 29.0 | 9.2 | 3.2 |
| Total | 598.8 | 118.9 | 5.0 |
The result is a unit cost of $5.0 million per lane mile. However, in reality there is a significant difference in costs between the different projects, with most projects in the range of $2 to $4 million and a small number of more expensive projects. This may suggest a need to group pavements by system or surface type to better account for this variability.
An agency decides that to maintain consistency with its financial reporting, the agency should use historic costs rather than current replacement cost. However, historic cost data are not consistently available. Thus, the agency decides to use the Wooster Method to estimate historic costs. Table 4-3 shows the application of this method for a selected set of assets using unit cost of $5 million per lane mile (as obtained in Example 4-1). The unit cost developed as described in Example 4-1 is applied and deflated to estimate historic costs. In this hypothetical example the total replacement cost is $3.9 billion in constant 2020 dollars and $2.0 billion in year of expenditure (historic) dollars.
Table 4-3. Estimation of Historic Costs of Pavement Reconstruction
| Route | Lane Miles (LM) | Year Constructed | 2020 Cost ($M) | Historic Cost ($M) |
|---|---|---|---|---|
| 11 | 96 | 2001 | 480.0 | 265.5 |
| 11 | 128 | 2004 | 640.0 | 397.1 |
| 22 | 72 | 1989 | 360.0 | 144.9 |
| 22 | 192 | 1996 | 960.0 | 470.5 |
| 33 | 32 | 2000 | 160.0 | 86.8 |
| 44 | 44 | 2003 | 220.0 | 128.4 |
| 44 | 8 | 1997 | 40.0 | 20.3 |
| 55 | 128 | 1990 | 640.0 | 264.1 |
| 66 | 28 | 2001 | 140.0 | 77.4 |
| 77 | 52 | 1999 | 260.0 | 137.4 |
| Total | 3,900.0 | 1,992.7 |
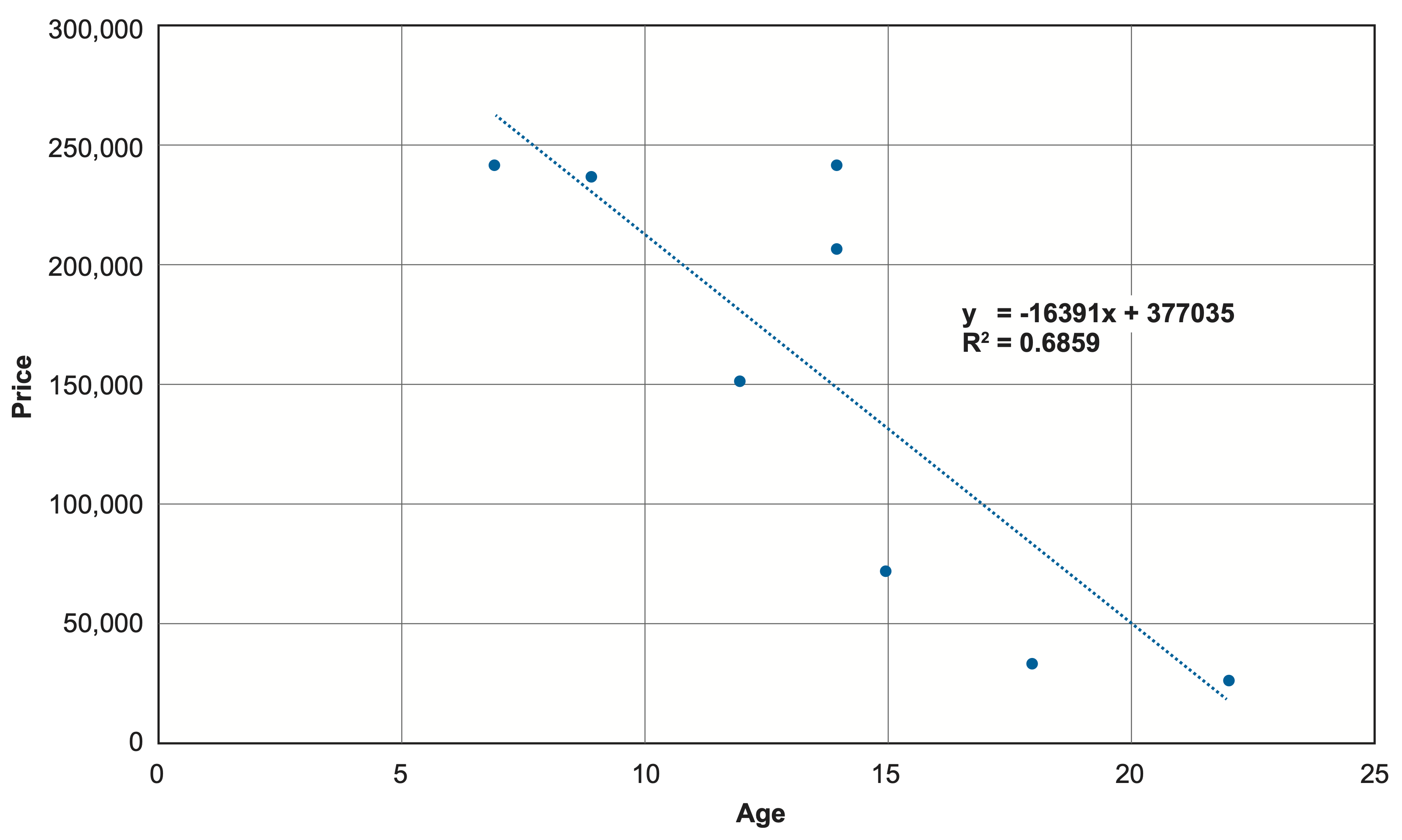
A transit agency has a fleet of over-the road transit buses purchased at different times from the same manufacturer. The agency seeks to establish the value of these buses using market value. Table 4-4 is a list of used coach buses from a selected manufacturer available for sale from an online bus reseller. It shows the age, mileage and price of each bus offered for sale.
Table 4-4. Over-the-Road Coach Buses Available for a Selected Manufacturer and Reseller
| Bus | Age (years) | Mileage | Prices ($) |
|---|---|---|---|
| 1 | 7 | 650,000 | 239,900 |
| 2 | 9 | 181,000 | 234,900 |
| 3 | 12 | 288,000 | 149,900 |
| 4 | 14 | 305,000 | 204,900 |
| 5 | 14 | 399,899 | 239,900 |
| 6 | 15 | 350,000 | 69,900 |
| 7 | 18 | 550,567 | 32,500 |
| 8 | 22 | not listed | 25,000 |
The agency uses the data in the table to construct a simple linear model for predicting the price of a used bus. In this case, price is predicted as a function of age using the following relationship:
Price = 377,035 - 16,391 * Age
Figure 4-2 shows the resulting model.
Note that alternative models were tested including both mileage and age, and substituting mileage for age. In this case the age-based model provides the best fit. In practice price may depend on a number of age, mileage, and other variables.
An agency is interested in using asset value to help prioritize reconstruction of a set of bridges to improve resilience. After discussing the cost, market and economic perspectives on asset value, agency leadership determines that the economic perspective is needed for this application. This perspective can help compare the benefits to society of reconstructing different bridges. Agency staff adapt the bridge screening approach established in FHWA’s National Bridge Investment Analysis System (NBIAS) to estimate asset value (32).
The approach used by NBIAS is to calculate the benefit of a bridge as the savings in travel and operating costs relative to that which would be incurred if all vehicles were detoured around the bridge. The calculation is made for autos and truck, and summed over time, applying a discount rate. The approach utilizes data available for U.S. highway bridges in the National Bridge Inventory (NBI) along with a small number of additional parameters. The following equations detail the calculation:
\begin{align*} B_a &= 365.25*T [ \frac{\tau}{100}(L C_l^t + \frac{L}{v_d} C_h^t) + (\frac{100-\tau}{100})(L C_l^t + \frac{L}{v_d} C_h^c)] \\ B &= B_a \sum_{i=1}^{N} \delta^{(i-1)} \end{align*}
where: